C++ 순열과 조합 Permutation, Combination
Intro
“코딩테스트” 라는것을 공부한지도 이제 두달이 넘어가고, 풀었던 문제도 100문제는 족히 넘어보인다.
이제는 낯설었던 프로그래밍언어와 어느정도 친숙해졌고, 문제를 보면 어떤방향으로 나아가야할 지도
보이는것같다.
오늘 정리할내용은 순열(Permutation)과 조합(Combination)이다. 수학은 고등학생때를 마지막으로 거의 공부한 적 없는것같은데 코딩테스트에서 필요할줄은 몰랐다.
코딩테스트 문제를 풀다보면 가끔 순열과 조합을 사용해야할 때가 있다. 하지만 이제는 기억조차 나지않을 정도로
공부한 지 오래된 내용이기도하고, 이것을 코드로 어떻게 구현할 지도 모르겠어서 정리해보려고 한다.
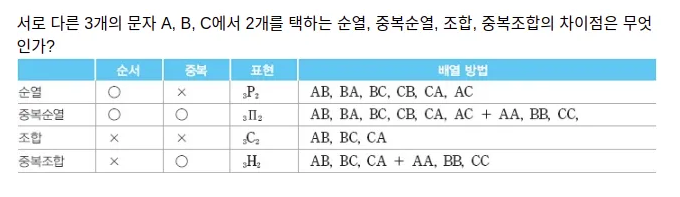
순열 Permutation
순열이란 “순서”의 개념이 존재하는 조합이다.
다른말로 “서로 다른 n개의 원소에서 r개를 선택한 후, 이를 나열하는 모든 경우의 수”로 말할 수 있다.
/*
예를들어 집합 { 1, 2, 3 } 가 있을 때, 이 3개의 원소로 만들 수 있는 모든 순열의 집합은
{ 1, 2, 3 }, { 1, 3, 2 }, { 2, 1, 3 }, { 2, 3, 1 }, { 3, 2, 1 }, { 3 , 1 , 2}
총 6개의 경우가 나올 수 있다.
*/
- 순서가 존재하기 때문에 { 1, 2, 3 }과 { 1, 3, 2 }는 다른 경우의 수가 된다.
순열 구현
먼저, 순서가 존재하고 중복은 허용하지 않는 순열이다.
재귀호출을 사용하여 구현하였다.
#include <iostream>
using namespace std;
// { 1,2,3,4 } 에서 3가지를 선택하는 경우의 수 4P3
#define n 4
#define r 3
int pArr[r];
int cnt; // 총 경우의 수
bool check[n + 1]; // 중복검사를 위한 배열
// 선택된 각 경우의 수 출력
void PrintArray(int arr[], size_t size)
{
for (int i = 0;i < size;i++)
{
cout << arr[i] << " ";
}
cnt++;
cout << "\n";
}
// 재귀호출을 사용한 순열
void Permutation(int depth) {
if (depth == r) {
PrintArray(pArr, r);
return;
}
for (int i = 1; i <= n; i++) {
if (!check[i]) {
check[i] = true;
pArr[depth] = i;
Permutation(depth + 1);
check[i] = false;
}
}
}
int main() {
cout << "순열 (순서o, 중복x)\n";
Permutation(0);
cout << "총 경우의수 : " << cnt << "개";
}
- 선택하고자하는 갯수 r에 도달하게된다면 끝이나게된다.
- depth는 현재 탐색하고있는 인덱스로,
- 중복을 허용하지 않으므로, check라는 중복방지 배열이 필요하다.
- check 배열을 통해 이미 고른 원소를 다시 고르지 않도록 한다.
- 순서가 존재하므로, 반드신 원소배열의 첫번째부터 탐색한다.
- 즉 {A,B,C} 라는 원소가 존재할 때 (A,A) -> (A,B) -> (A,C) 탐색 이후
- (B,A) -> (B,B) 순으로 탐색하게된다.
- 이때 check 배열을 통해 중복된 원소를 선택한 경우는 걸러지게된다.
다음으로 중복가능한 순열을 구현해보았다.
#include <iostream>
using namespace std;
// { 1,2,3,4 } 에서 3가지를 선택하는 경우의 수
#define n 4
#define r 3
int dpArr[r];
int cnt; // 총 경우의 수
// 선택된 각 경우의 수 출력
void PrintArray(int arr[], size_t size)
{
for (int i = 0;i < size;i++)
{
cout << arr[i] << " ";
}
cnt++;
cout << "\n";
}
// 재귀호출을 사용한 순열
void DuplicatePermutation(int depth) {
if (depth == r) {
PrintArray(dpArr, r);
return;
}
for (int i = 1; i <= n; i++) {
dpArr[depth] = i;
DuplicatePermutation(depth + 1);
}
}
int main() {
cout << "순열 (순서o, 중복o)\n";
DuplicatePermutation(0);
cout << "총 경우의수 : " << cnt << "개";
}
- 중복검사를 할 필요가없으므로, check 배열이 필요없다.
조합 Combination
조합이란 “순서”의 개념없이 “서로 다른 n개의 원소에서 r개를 선택한 후, 이를 나열하는 모든 경우의 수”로 말할 수 있다.
/*
예를들어 집합 { 1, 2, 3 } 가 있을 때, 이 3개의 원소로 만들 수 있는 모든 조합의 집합은
{ 1, 2, 3 }
총 1개의 경우가 나올 수 있다.
*/
- 순서가 존재하지 않기 때문에 { 1, 2, 3 } , { 1, 3, 2 } , { 2, 1, 3 }… 등 모두 같은 경우가 된다.
조합 구현
먼저 중복을 허용하지 않는 조합이다.
마찬가지로 재귀호출을 사용하여 구현했으며, 반복문을 돌며 모든 경우에 대해 선택하는것은 같으나
반복문의 시작 값은 이전에 선택한 값 + 1 이 된다.
#include <iostream>
using namespace std;
// { 1,2,3,4 } 에서 3가지를 선택하는 경우의 수 4C3
#define n 4
#define r 3
int cArr[r]; // 선택된 원소들
int cnt; // 총 경우의 수
bool check[n + 1];
// 선택된 각 경우의 수 출력
void PrintArray(int arr[], size_t size)
{
for (int i = 0;i < size;i++)
{
cout << arr[i] << " ";
}
cnt++;
cout << "\n";
}
// 재귀호출을 사용한 조합
void Combination(int depth, int cnt) {
if (cnt == r) {
PrintArray(cArr, r);
return;
}
for (int i = depth; i <= n; i++) {
if (!check[i]) {
check[i] = true;
cArr[cnt] = i;
Combination(i + 1, cnt + 1);
check[i] = false;
}
}
}
int main() {
cout << "조합 (순서x, 중복x)\n";
Combination(1, 0);
cout << "총 경우의수 : " << cnt << "개";
}
- 조합은 순서가 존재하지 않으므로 현재 인덱스 이전의 원소는 신경쓰지않는다.
- 즉, (A,A) -> (A,B) -> (A,C) 이후 (B,A)를 탐색하는것이 아닌 (B,B) -> (B,C) 로 바로 넘어가게된다.
- depth는 현재 탐색할 인덱스, cnt는 선택한 원소 갯수다.
다음으로 중복을 허용하는 조합이다.
#include <iostream>
using namespace std;
// { 1,2,3,4 } 에서 3가지를 선택하는 경우의 수 4H3
#define n 4
#define r 3
int cArr[r]; // 선택된 원소들
int cnt; // 총 경우의 수
// 선택된 각 경우의 수 출력
void PrintArray(int arr[], size_t size)
{
for (int i = 0;i < size;i++)
{
cout << arr[i] << " ";
}
cnt++;
cout << "\n";
}
// 재귀호출을 사용한 조합
void Combination(int depth, int cnt) {
if (cnt == r) {
PrintArray(cArr, r);
return;
}
for (int i = depth; i <= n; i++) {
cArr[cnt] = i;
Combination(i, cnt + 1);
}
}
int main() {
cout << "조합 (순서x, 중복o)\n";
Combination(1, 0);
cout << "총 경우의수 : " << cnt << "개";
}
- 마찬가지로 중복을 검사하는 부분이 빠졌다.
순열 표준라이브러리
-
C++ 에서 순열을 구성하는 또다른 방법으로, 라이브러리를 사용하는것이다.
-
algorithm 헤더를 포함시키면 사용할 수 있다.
- next_permutation : “오름차순의 배열”을 기반
- prev_permutation : “내림차순의 배열”을 기반
-
매개변수로 (first, last) 범위로 순열을 시작할 범위의 첫번째 주소, 그리고 포함되지 않는 마지막 주소를 넣는다.
-
매개변수로 iterator를 받기때문에 string 타입의 변수도 순열을 구할 수 있다.
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
string s = "4231";
vector<int> v = { 3, 1, 2 };
// 오름차순 정렬
sort(s.begin(), s.end());
sort(v.begin(), v.end());
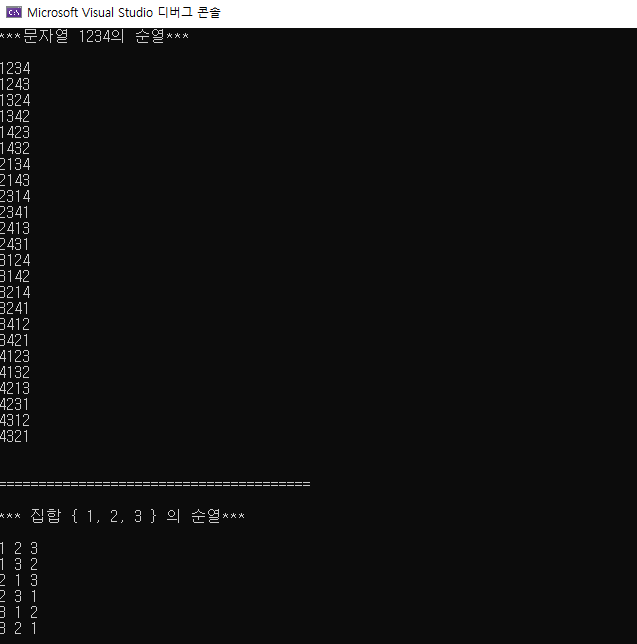
cout << "***문자열 " << s << "의 순열***\n\n";
// 문자열 s의 순열
do {
cout << s << "\n";
} while (next_permutation(s.begin(), s.end()));
cout << "\n\n=======================================\n\n";
cout << "*** 집합 { 1, 2, 3 } 의 순열***\n\n";
do {
for (int i = 0;i < v.size();i++)
cout << v[i] << " ";
cout << "\n";
} while (next_permutation(v.begin(), v.end()));
}
-
next_permutation 함수는 오름차순 정렬이된 데이터를 사용해야한다.
-
next_permutation 함수는 현재보다 더 큰 순열로 재배열할 수 있으면 반복하여 구해내는 구조로, while 문을 사용하여 반복하였다.
-
만약 데이터가 내림차순으로 정렬되어 있다면 prev_permutation 함수를 사용하면 된다.
댓글남기기