백준 1149 C++ - RGB거리

Intro

문제해결 및 소스코드

#include <iostream>
#include <algorithm>

using namespace std;

/*									<문제해결>
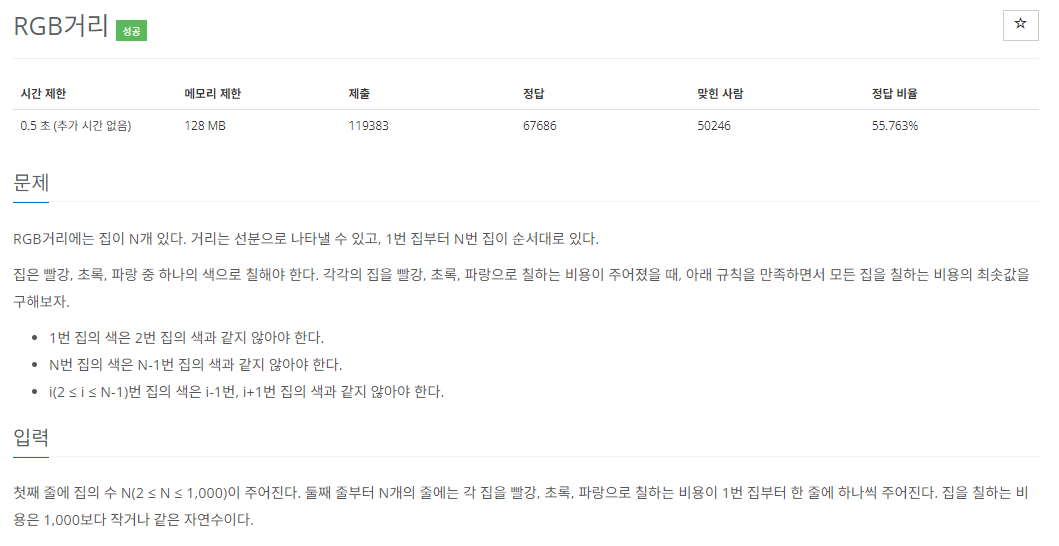
				규칙1. 인접한 집의 색은 같으면 안된다.

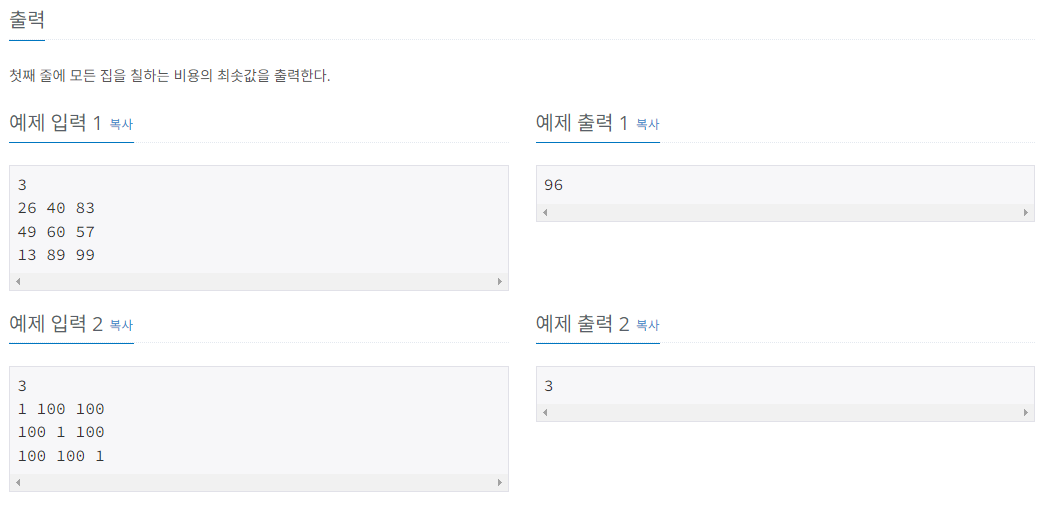
				문제해결을 위해 예제입력1로 예를들었다.
				3번째 집까지 칠하는데 최소비용을 구하려면, 2번째집까지 칠하는데 최소비용 + 3번째집을 연속되지 않은색으로 칠하는 비용 중
				최소를 고르면 된다. 즉 다음계산을위해 이전의 계산이 필요한 DP방식의 문제라고 생각했다.

				문제해결을 위해 먼저, 테이블을 설정한다.
				1. dp[i][j] = i번째 집을 j색깔로 칠하는데 드는 최소비용 => j는 3가지가 될것이다(R,G,B)
				2. cost[i][j] = i번째 집을 j색깔로 칠하는데 드는 비용 

				그다음, 점화식을 찾아낸다. j : 0, 1, 2 => R, G, B라고 생각했다.
				dp[i][0] = cost[i][0] + min(dp[i-1][1] + dp[i-1][2])	: i번째집을 Red로 칠했을 때는 i번째비용 + 이전단계의 최소비용(색깔이 연속되지 않는)
				dp[i][1] = cost[i][1] + min(dp[i-1][0] + dp[i-1][2])
				dp[i][2] = cost[i][2] + min(dp[i-1][0] + dp[i-1][1])

				마지막으로 기저값을 설정한다.
				dp[1][0] = cost[1][0]
				dp[1][1] = cost[1][1]
				dp[1][2] = cost[1][2]

				최종 답은 n번째 집을 칠했을 때의 최소비용이므로 min(dp[n][0], dp[n][1], dp[n][2])가 된다.
*/

int cost[1001][3];			// .. 집을 칠하는 비용을 담을 배열
int dp[1001][3];			// .. n번째 집까지 칠하는 최소비용을 담을 배열

int main()
{
	int n;
	cin >> n;

	// .. 비용입력
	for (int i = 1;i <= n;i++)
	{
		for (int j = 0;j < 3;j++)
		{
			cin >> cost[i][j];
		}
	}
	
	// .. 기저값 설정
	for (int j = 0;j < 3;j++)
	{
		dp[1][j] = cost[1][j];
	}

	for (int i = 2;i <= n;i++)
	{
		dp[i][0] = cost[i][0] + min(dp[i - 1][1], dp[i - 1][2]);
		dp[i][1] = cost[i][1] + min(dp[i - 1][0], dp[i - 1][2]);
		dp[i][2] = cost[i][2] + min(dp[i - 1][0], dp[i - 1][1]);
	}

	cout << min(dp[n][0], min(dp[n][1], dp[n][2]));
}