백준 15989 C++ - 1, 2, 3 더하기 4

Intro

문제해결 및 소스코드

• 1, 2, 3 더하기 시리즈의 4번째 문제입니다.

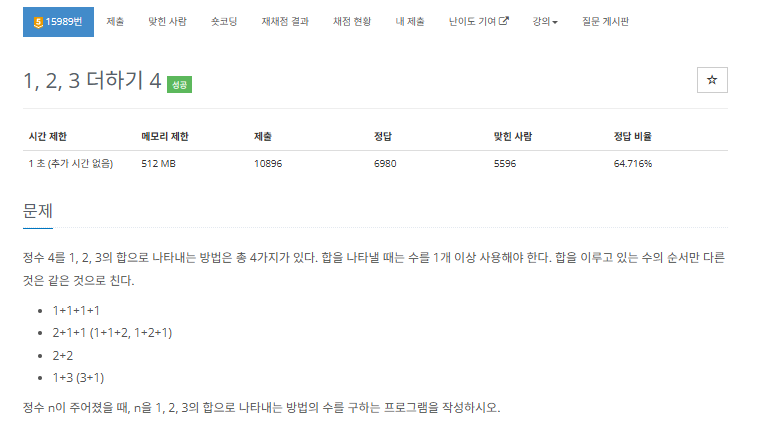
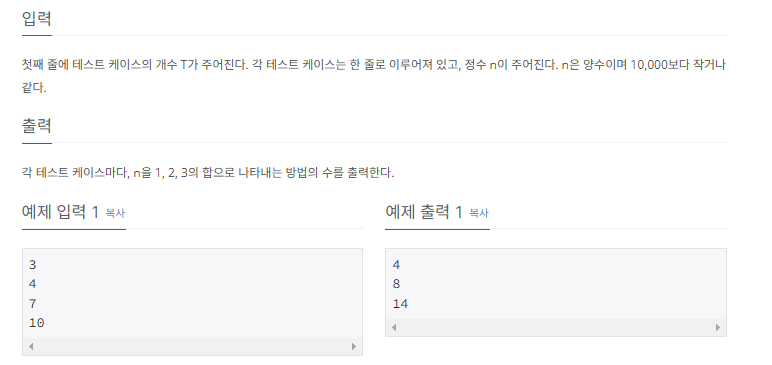
• 입력되는 어떤 수 N을 1, 2, 3의 합으로 나타내는 방법의 수를 출력해야하는데, 조합은 같고 순서만 다른것은 같은것으로 칩니다. 예를 들어 “1 + 1 + 2” 와 “1 + 2 + 1” 는 같은것입니다.

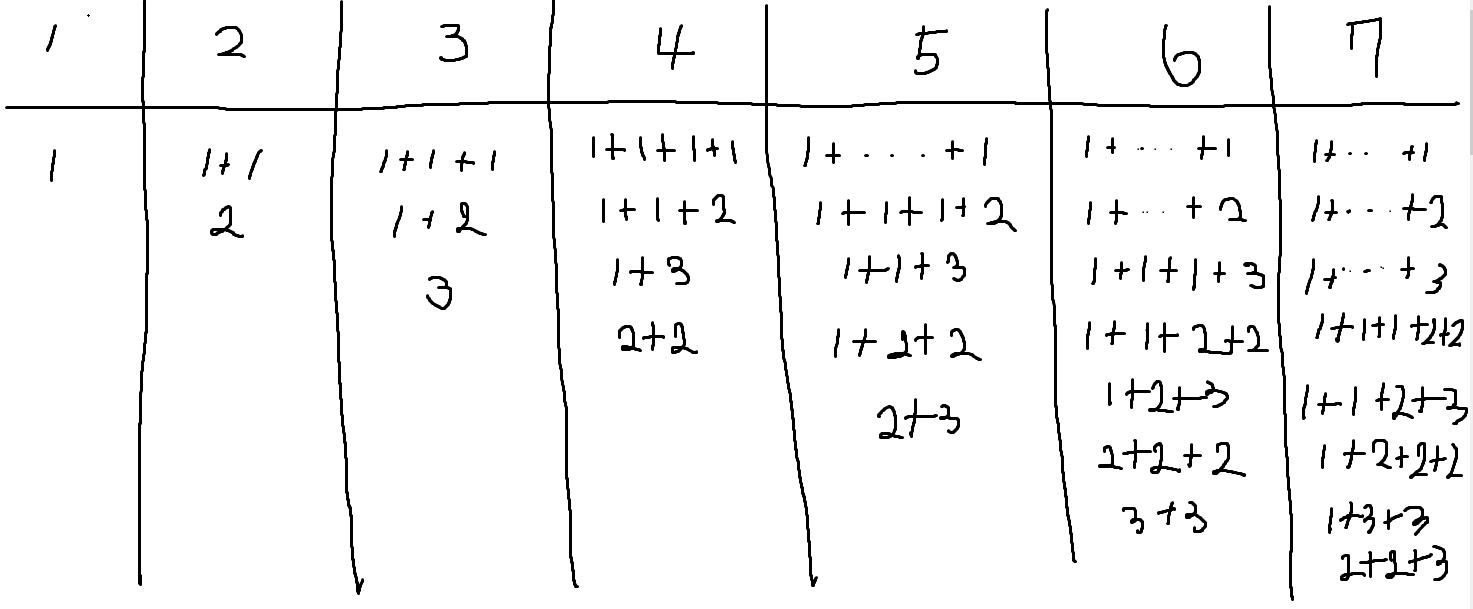
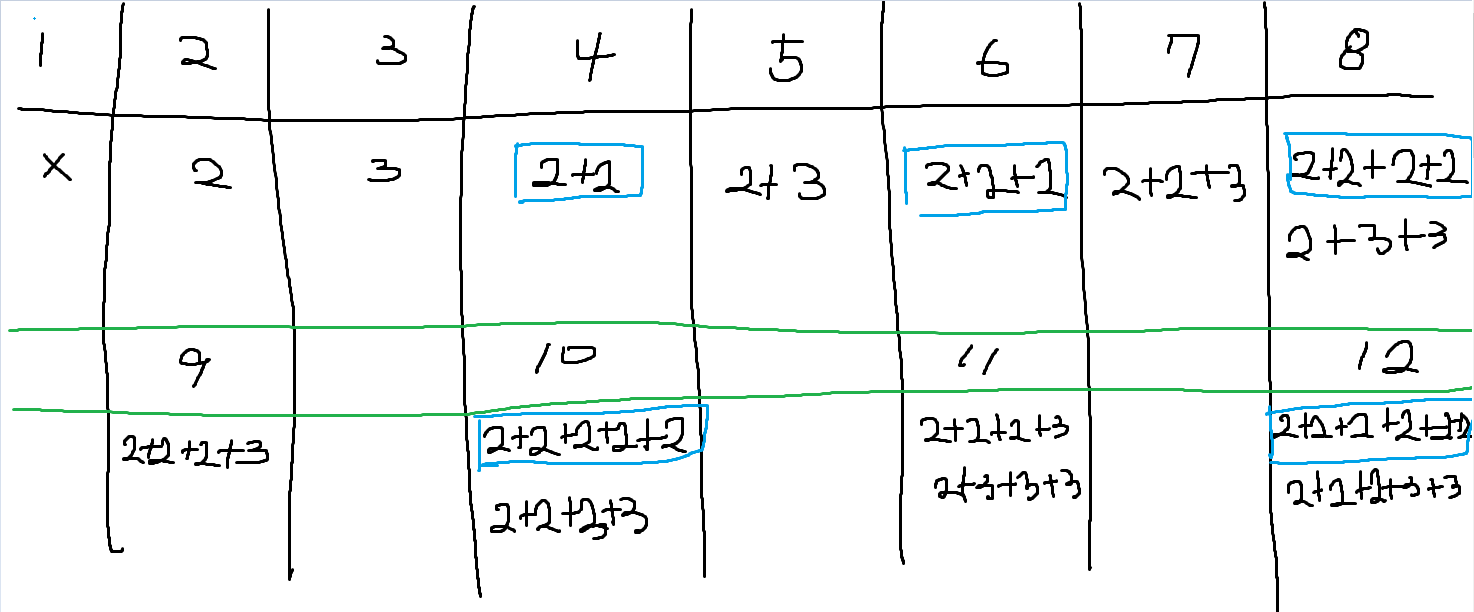
• 먼저, 문제의 규칙성을 찾기위해 몇가지 예를 작성해봤습니다.

• 규칙성이 보이시나요?

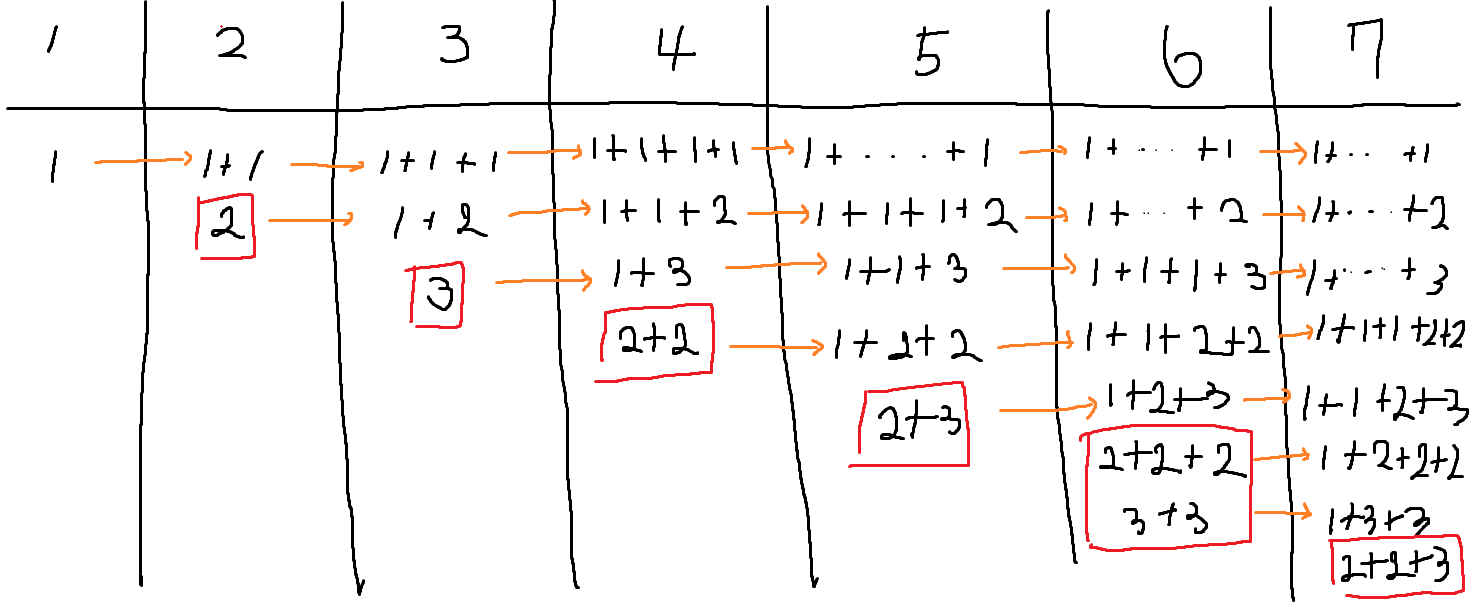
• 어떤 수를 만들려면 앞선수를 만드는 방법에다 +1을 해주면됩니다. 그리고 빨간색 네모는 앞선수에서는 없는 새로운 경우입니다.

• 그런데, 빨간색 네모의 조합은 2와 3만으로 이루어져있다는것을 발견했습니다.

• 따라서 빨간색 네모는 어떤수를 2와 3의 합으로 만드는 경우의수라는것을 알 수 있습니다.

• 마찬가지로 몇가지 예를 작성하고, 규칙성을 찾아봤습니다.

/*  
        공통특징 - 어떤수 N을 만드는 방법은 N-3을 만드는방법에 +3을 한것과 같다.  

        짝수일 경우 - 무조건 '2'로만 이루어진 조합이 있다.

        예를들어, 
                    8은 '2'로만 이루어진 조합 1개와,
                    5를[8-3] 만드는 조합에 +3을한 조합1개로 총 2개가 됩니다.
*/

1. 따라서 이 문제를 해결하기위해서 먼저, 어떤수 N을 2와 3의 합으로 만드는방법을 구해주고,

2. 최종적으로 “N-1을 만드는 방법 + (1)의 방법” 으로 답을 구할 수 있습니다.

#include <iostream>
#define MAX 10000

using namespace std;

int tot[10001];				// tot[i] i를 2와 3으로 만들수 있는 경우의 수
int dp[10001];				// 최종 답

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int n;
	cin >> n;

	// 초기값 설정
	dp[1] = 1;
	dp[2] = 2;
	dp[3] = 3;

	tot[2] = 1;
	tot[3] = 1;

	for (int i = 4;i <= MAX;i++)
	{
		// 짝수일경우
		if (i % 2 == 0)
			tot[i] = 1 + tot[i - 3];
		else
			tot[i] = tot[i - 3];

		dp[i] = dp[i - 1] + tot[i];
	}

	
	for (int i = 1;i <= n;i++)
	{
		int input;
		cin >> input;
		cout << dp[input] << "\n";
	}
}