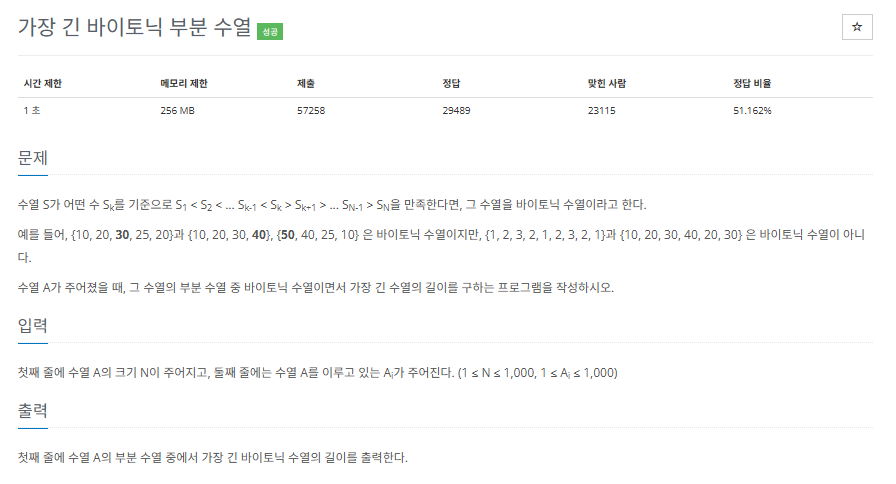
백준 11054 C++ - 가장 긴 바이토닉 부분 수열

Intro

문제해결 및 소스코드

• 이 문제는 가장 긴 증가하는 부분 수열문제, 가장 긴 감소하는 부분 수열문제를 응용하여 해결할 수 있는 문제이다.

• 아직 접해보지 않았다면 먼저 해당 문제를 해결해보는것이 좋다.(11053번, 11722번)

• 바이토닉 부분 수열이란, 수열이 주어졌을 때 어떤 수를 기준으로 좌측에서는 증가하고, 우측에서는 감소하는 수열이다.

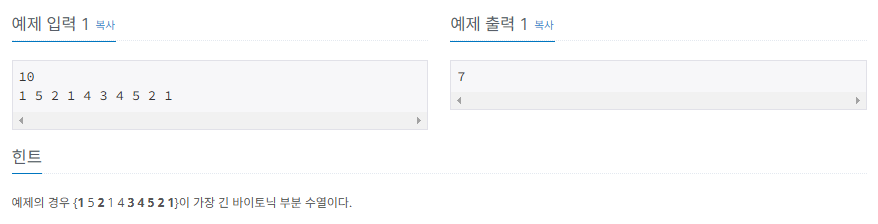
/*                  예제1. 
    주어진 수열 { 1 5 2 1 4 3 4 5 2 1 } 에서, 가장 긴 바이토닉 부분수열은 
    { 1  2   3 4 5 2 1 } 로 길이가 7이다.
*/ 

• 그렇다면 이 문제는 어떻게 해결해야될까? 예를들어 수열 { 1 2 3 2 1 } 이 있다고 하자.

• 수열의 각 원소에 대하여 증가하는 부분수열과 감소하는 부분수열이 있을것이다.

• 이때, 가장 긴 바이토닉 부분수열은 “각 원소에 대한 증감 부분수열의 길이의 최대합 - 1” 이 된다.

• -1 을 해주는 이유는, 해당 원소에서의 증가 및 감소하는 부분수열 구하면서 중복 사용되었기 때문이다.

#include <iostream>
#include <algorithm>

using namespace std;

int arr[1001];				// 수열
int dp[1001];				// 증가하는 부분수열
int r_dp[1001];				// 감소하는 부분수열


int main()
{
	int n;
	cin >> n;

	// 입력
	for (int i = 1;i <= n;i++)
	{
		cin >> arr[i];
		dp[i] = 1;
		r_dp[i] = 1;
	}

	// 1. 각 원소의 가장 긴 증가하는 부분수열
	for (int i = 1;i <= n;i++)
	{
		for (int j = 1;j < i;j++)
		{
			if (arr[i] > arr[j]) dp[i] = max(dp[i], dp[j] + 1);
		}
	}

	// 2. 각 원소의 가장 긴 감소하는 부분수열
	for (int i = n;i > 0;i--)
	{
		for (int j = n;j > i;j--)
		{
			if (arr[i] > arr[j]) r_dp[i] = max(r_dp[i], r_dp[j] + 1);
		}
	}

	int ans = 0;
	// 3. 증가하는 부분수열과 감소하는 부분수열의 최대합 구하기
	for (int i = 1;i <= n;i++)
	{
		if (ans < dp[i] + r_dp[i]) ans = dp[i] + r_dp[i] - 1;		// 중복제거
	}

	cout << ans;
}