DFS(깊이우선탐색)와 BFS(너비우선탐색)
Intro
- 이번포스팅에서는 DFS와 BFS 알고리즘에 대해 공부한 내용을 기록했습니다.
- DFS와 BFS 알고리즘은 “재귀함수호출”과 “큐”에 대한 이해가 필요합니다.
DFS의 이해
- DFS(Depth First Search) 알고리즘은 그래프 전체를 탐색하는 방법중 하나로, 시작점부터 다음 정점으로 넘어가기 전에 해당 정점을 완전히 탐색하고 넘어가는 방법입니다.
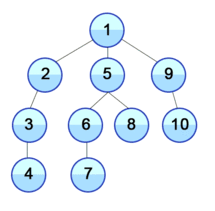
- 위 같은 그래프가 있다고 할 때,
- 시작점(1) 부터 탐색을 시작하여 시작점과 연결된 다른 노드들 중 작은노드(2)를 다음으로 탐색합니다.
- 정점(2)에는 또 다른 정점(3)이 있으므로 정점(3)을 다음으로 탐색합니다.
- 마지막으로 정점(3)과 연결된 정점(4)를 탐색한 뒤, 시작점(1)과 연결된 또 다른 노드(5)를 다음으로 탐색합니다.
- 위와 같은 방식으로 모든 정점들을 탐색하면 그 순서는 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 이 됩니다.
구현방법
- DFS 알고리즘은 재귀함수 또는 스택으로 구현합니다.
1. 탐색 시작 노드를 스택에 삽입하고, 방문처리
2. 스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도있다면 그 노드를 스택에 넣고 방문처리
3. 방문하지 않은 인접한 노드가 없으면 스택에서 최상단 노드를 꺼냄.
4. 위 과정을 수행할 수 없을 때까지 반복
- 여기서 중요한 것은 노드 방문 시 방문여부(Visited)를 반드시 검사해야하는것입니다. 그렇지 않으면 무한루프에 빠질 수 있기 때문입니다.
BFS의 이해
-
BFS(Breadth First Search) 알고리즘은 시작 노드를 방문한 후 시작 노드에 있는 인접한 모든 노드들을 우선 탐색하는 방법입니다.
-
더 이상 방문하지 않은 노드가 없을 때까지 방문하지 않은 모든 노드에 대해서도 BFS를 적용합니다.
- 마찬가지로 위의 예시를 들면
- 시작점(1) 부터 탐색을 시작하여 시작점과 연결된 다른 노드들 중 작은노드(2)를 다음으로 탐색합니다.
- 그 다음으로 작은노드(5),(9)를 탐색합니다.
- 시작점과 연결된 노드들을 모두 탐색했으므로, 노드(2)와 연결된 노드부터 탐색을 합니다.
- 위와 같은 방식으로 모든 정점들을 탐색하면 그 순서는 1 - 2 - 5 - 9 - 3 - 6 - 8 - 10 - 4 - 7 이 됩니다.
구현방법
- BFS는 자료구조중 큐를 이용하여 구현합니다.
1. 탐색 시작 노드를 큐에 삽입하고 방문처리
2. 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중 방문하지 않은 노드를 모두 큐에 삽입 후 방문처리
3. 2번을 반복
- BFS 알고리즘도 마찬가지로 노드 방문 시 방문여부(Visited)를 반드시 검사해야합니다.
- BFS 알고리즘은 특정 조건의 최단 경로 알고리즘을 계산할 때 사용합니다.
DFS와 BFS 코드 C++
- 백준 1260번 문제인 DFS와 BFS를 예시로 코드를 작성했습니다. 이 문제는 DFS와 BFS의 기본적인 구현을하는 문제입니다.
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
/* <문제해결>
[DFS 구현]
각 정점에서의 간선을 표현한다. 2차원벡터를 이용하여 표현
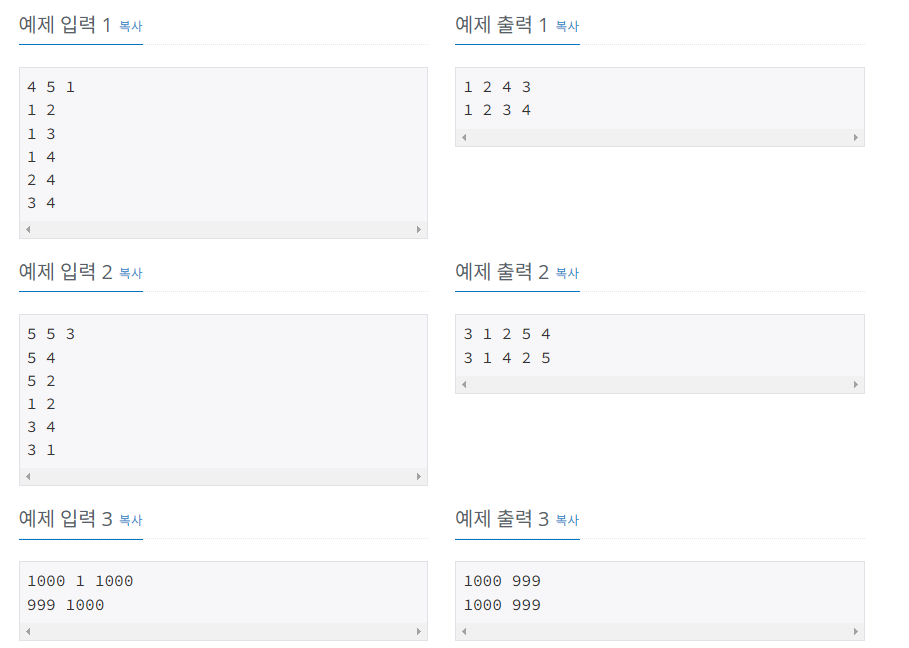
예시) 5개의 정점, 간선 (5,4) (5,2) (1,2) (3,4) (3,1) 입력, 비방향그래프
아래의 의미는 각 정점(1~5)에서 갈 수 있는 정점이 어디인가?
graph[1] = { 2, 3 } ex) 정점1에서는 2,3번 정점으로 갈 수 있음
graph[2] = { 1, 5 }
graph[3] = { 1, 4 }
graph[4] = { 3, 5 }
graph[5] = { 2, 4 }
탐색시작 정점(v)부터 시작하여, 재귀호출을 이용한 구현.
visited 배열 => 해당 정점을 방문했는지 판단하기위한 배열
과정)
DFS(탐색시작정점) => 먼저 해당정점을 방문했음을 기록 visited[탐색시작정점] = true
그 다음, 해당 정점에서 갈 수 있는 다른 정점을 확인하는데, 방문한적 없다면 DFS를 재귀호출.
[BFS 구현]
위의 예시와 같은 케이스
탐색시작 정점(v)부터 시작하여, 큐를 이용한 구현.
과정)
BFS(탐색시작정점) => 먼저 해당정점을 방문했음을 기록 visited[탐색시작정점] = true.
큐를 하나 만들어, 첫 정점을 큐에넣고 while문을 통해 큐가 빌 때까지 아래를 반복
큐의 front(먼저들어온(작은수우선))를 뽑아 해당 정점에서 갈 수 있는 다른 정점을 확인하는데, 방문한적 없다면 큐에 넣음.
*/
vector<int> graph[1001]; // .. 그래프
bool visited_DFS[1001]; // .. 해당노드를 방문했는지 여부(DFS)
bool visited_BFS[1001]; // .. 해당노드를 방문했는지 여부(BFS)
void DFS(int startNode)
{
visited_DFS[startNode] = true;
cout << startNode << " ";
// 해당 노드와 연결된 다른노드 탐색
for (int index = 0;index < graph[startNode].size();index++)
{
int temp = graph[startNode][index];
if (visited_DFS[temp] == false)
DFS(temp);
}
}
void BFS(int startNode)
{
queue<int> que;
visited_BFS[startNode] = true;
que.push(startNode);
while (!que.empty())
{
int x = que.front();
que.pop();
cout << x << " ";
// 해당 노드와 연결된 다른노드 탐색
for (int index = 0;index < graph[x].size();index++)
{
int y = graph[x][index];
if (visited_BFS[y] == false)
{
visited_BFS[y] = true;
que.push(y);
}
}
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
int n, m, v; // .. 정점갯수, 간선갯수, 시작정점
cin >> n >> m >> v;
// 비방향 간선 입력
for (int i = 1;i <= m;i++)
{
int start, end;
cin >> start >> end;
graph[start].push_back(end);
graph[end].push_back(start);
}
// 오름차순 정렬(낮은수부터 탐색하도록)
for (int i = 1; i <= n;i++)
{
sort(graph[i].begin(), graph[i].end());
}
DFS(v);
cout << "\n";
BFS(v);
}
댓글남기기